It wasn't quite clear to me what the logical dependencies were in the CAPM (Capital Asset Pricing Model). I looked into it, and have written up my thoughts below.
Here is the main conclusion of the CAPM:
(MC)
![]()
where p is any portfolio of assets, E[ r(p) ] the expected return of that portfolio, beta_m(p) the market beta of that portfolio, E[ rm ] the expected return of the market portfolio, and r0 essentially the risk free rate (if no risk free asset exists, the equation still holds by setting r0 to the expected return of the zero covariance portfolio of the market portfolio).
In other words, the expected excess return (i.e., return above r0) of any portfolio is equal to the beta of the portfolio times a constant, namely the expected excess return of the market portfolio. Thus, a portfolio with a beta of one has the same expected return as the market portfolio, while a portfolio with zero beta has an expected return equal to the risk free portfolio.
Definitions
Some quick definitions that come in handy:
- An m-v-efficient portfolio is a portfolio of assets that has the minimum variance for a given expected return (also called a frontier portfolio, because if we plot mean and variance of all possible portfolios, the m-v-efficient portfolios will constitute the (parabolic) frontier of that shape).
- The beta of a portfolio p with respect to some other portfolio m is:
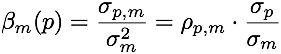 where sigma(p,m) denotes covariance between p and m, sigma^2(m) the variance, rho correlation, and sigma(x) the standard deviation of x.
where sigma(p,m) denotes covariance between p and m, sigma^2(m) the variance, rho correlation, and sigma(x) the standard deviation of x. - The market portfolio is the sum (or portfolio) of all portfolios of the individual investors.
The main conclusion of the CAPM (MC) follows immediately from the following:
- 1) The market portfolio is m-v-efficient.
That's really it. The rest is mathematics. (Of course, there are all these idealised world assumptions: no transaction costs, finite set of assets with finite expectation and variance, homogenous expectations (that is, all investors agree on the expected returns and variance-covariance matrix of the assets), shorts sales of all assets allowed, no arbitrage, etc. etc.) But, the main conclusion above rests ONLY on the mean-variance efficiency of the market portfolio, and is a direct mathematical consequence of that.
In particular, two things hold true just by looking at the mathematics of expectation and variance of portfolios.
Mathematics
- A) The set of m-v-efficient portfolios is convex (whether or not there is a risk-free asset). That means that any combination (or portfolio) of m-v-efficient portfolios is again an m-v-efficient portfolio.
- B) Fix any m-v-efficient portfolio m. Then, for any portfolio p, there is is a linear relationship between the expected return of p and the beta of p with respect to m. This is rather remarkable: the linear relationship between return and beta of portfolios holds with respect to any m-v-efficient portfolio.
So, all one needs for (MC) to hold is above 1., that the market portfolio is an m-v-efficient portfolio (then the linear relationship of return and beta, which holds with respect to any m-v-efficient portfolio (by mathematics B)) holds with respect to the market portfolio). Now, under what circumstances is the market portfolio going to be m-v-efficient? Well, easy, let's introduce the next two assumptions:
- 2) All investors are m-v investors, that is, their preference involves only mean and variance of a portfolio (in particular, the more mean for given variance, the better).
- 3) The market clears, equilibrium prevails.
Now, 2) implies that all investors wish to hold m-v-efficent portfolios. The market clearing assumption 3) means that all investors do indeed hold m-v-efficient portfolios. Then, by the convexity of m-v-efficient portfolios (mathematics A)), the market portfolio is m-v-efficient, so we have 1), thus we have (MC).
The question arises then: Are investors m-v investors? A few things to note:
- m-v preference is sometimes understood to be a special case of expected utility maximisation (EUM). Indeed, it can obtain under certain conditions: one needs to impose conditions on either a) the distribution of returns, or b) the utility function of investors, or c) joint conditions on both (essentially cutting off the Taylor expansion of the expected utility after a few terms).
- a) When returns are normally distributed, m-v preference holds under EUM. This is clearly not a very realistic assumption (it excludes assets with limited liability, for example, and does not allow for large jumps as frequently as they are observed in reality). However, one can generalise this to elliptically distributed returns (such as multivariate normal, student-t, or even Cauchy), as shown by G. Chamberlain in 1983 (these allow both fatter tails, if desired, or limited liability assets).
- b) For arbitrary returns distribution, investors are still m-v investors if the utility function is quadratic, as Harry Markovitz pointed out already in 1952. This is clearly not very realistic, as utility is not monotonically increasing. Even if restricted to the increasing arm of the parabola, quadratic utility displays increasing absolute risk aversion, which is not consistent with empirical results.
- c) The case of joint conditions on returns and distributions was examined in detail by Berk in 1997. It doesn't really allow for more realistic cases though.
- m-v preference has some problems:
- investors are presumed indifferent with respect to higher moments, e.g. the skew of a distribution, which is clearly unrealistic.
- investors might reject the addition of an asset with too high variance, even if it is of limited liability. (Imagine I offer you a free share of Facebook or some other other super volatile asset. It might drop to zero, or it might become quite valuable, but it has massive variance. Clearly, you'd take it for free, as there is only upside. A m-v investor, however, might reject it, if it increases his variance too much without sufficient increase in mean).
- it is not compatible with constant relative risk aversion, which is empirically quite plausible, as shown by Andreas Löffler in 1996.
- m-v preference follows from two fairly innocuous conditions, namely monotony in the risk free asset and variance aversion (the rejection of adding any noise portfolio that has zero mean and zero covariance to the existing portfolio), as shown by Andreas Löffler in 1996.
- All in all, m-v preference is fairly problematic, empirically implausible, and only really used because it is so simple and analytically tractable. Under EUM, one arrives not at the nice CAPM, but at general Arrow-Debreu style equilibrium models, which are hard to handle, and not particularly insightful.
Summary
So, to summarise, the logical structure of the CAPM is something like this:
- For some reason (EUM and elliptic asset distribution, or EUM and quadratic utility, or monotony & variance aversion) all investors have m-v-preference.
- By assumption, we achieve equilibrium, so all investors hold m-v-efficient portfolios.
- Then the market portfolio is m-v-efficient, by convexity of m-v-efficient portfolios (mathematics A,)
- Thus (by mathematics B, property of m-v-efficient portfolios) follows (MC): the expected excess return of any portfolio is its market beta times a constant (namely the expected excess return of the market portfolio)
But, all that is required for the main conclusion of the CAPM to hold is that the market portfolio is m-v-efficient (for whatever reason).
